Все Студенту - шпоры, доклады, рефераты, лабораторные, ргр

3), то определенное по прямой 3 значение момента сил трения М_тр , в соответствии с формулами (15) и (16), будет отрицательным (при этом крестовина должна начать вращение в сторону, противоположную приложенному моменту силы натяжения).

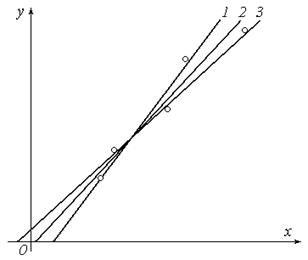
Рис.13.

Метод наименьших квадратов

Надежным и научно обоснованным способом определения коэффициентов экспериментальных зависимостей является метод наименьших квадратов. Суть его заключается в подборе таких значений коэффициентов, при которых сумма квадратов отклонений (СКО) измеренных в опытах значений y_i (i = 1, 2, …, n) от теоретических была минимальной.

Покажем, как подбираются значения коэффициентов K и b линейной зависимости у(х) вида (16). Найдем сумму квадратов отклонений

.

После раскрытия круглых скобок и возведения в квадрат получим

или

, (20)

где .

Из выражения (20) следует, что при различных значениях коэффициентов K и b величина S также будет принимать различные значения. Таким образом, СКО является функцией двух независимых переменных K и b. Для нахождения минимума функции S(K, b) необходимо приравнять к нулю ее частные производные:

Полученные выражения позволяют записать систему уравнений для отыскания «наилучших» значений коэффициентов K и b:

Решая эту систему, находим:

; (21)

, (22)

где

(23)

Обработку экспериментально полученных линейных зависимостей рекомендуется проводить в следующей последовательности:

1) для удобства выполнения расчетов составить таблицу (или дополнить таблицу экспериментальных данных) по образцу табл. 6;

Таблица 6

Номер опыта	…	Х	у	х 2	х у
1	…
2	…
…	…
п	…
	S =

2) измеренные (или рассчитанные с помощью измеренных величин) значения аргумента х и функции у занести в соответствующие столбцы таблицы;

3) для каждого i-го опыта (i = 1, 2, …, n) последовательно вычислить значения квадрата аргумента х_i² и произведения х_i y_i ; не округляя этих значений, занести их в два последних столбца таблицы;

4) рассчитать значения сумм S_x , S_y , S_xx , S_xy и, не округляя, записать в соответствующие ячейки строки «S = »;

5) по формулам (23), (21) и (22) вычислить значения коэффициентов линейной зависимости.