ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ЗАВИСИМОСТЕЙ часть 5
Пример 9. Используем метод наименьших квадратов для определения ЭДС аккумулятора E и его внутреннего сопротивления r (пример 8 на с. 23). Занесем данные табл. 5 во второй и третий столбцы табл. 7.
Таблица 7
| Номер опыта | I, A | U, B | I 2, A2 | I×U, A×B |
| 1 | 1,20 | 19,1 | 1,4400 | 22,920 |
| 2 | 1,35 | 15,5 | 1,8225 | 20,925 |
| 3 | 2,00 | 12,9 | 4,0000 | 25,800 |
| 4 | 2,40 | 11,5 | 5,7600 | 27,600 |
| 5 | 3,00 | 10,0 | 9,0000 | 30,000 |
| 6 | 4,00 | 4,3 | 16,0000 | 17,200 |
| S = | 13,95 | 73,3 | 38,0225 | 144,445 |
Вычисляя значения I 2 и I×U (без округления), заполним последние два столбца таблицы. Сложим числа по столбцам и занесем результаты в строку «S = ».
Учитывая соотношения (19), с помощью формул (23), (21) и (22) найдем ЭДС и внутреннее сопротивление аккумулятора:


E = 
Линеаризация нелинейных зависимостей
Описанный выше графический способ, а также полученные методом наименьших квадратов формулы (21)-(23) для расчета коэффициентов в ряде случаев могут быть использованы и при обработке нелинейных зависимостей. В первую очередь это относится к зависимостям, описываемым степенными и показательными (экспоненциальными) функциями. Для их линеаризации (приведения к линейному виду) применяется операция логарифмирования.
Степенная зависимость. Пусть измеряемые величины Х и Y теоретически связаны зависимостью вида
Y = C×X k,
где С и k – неизвестные коэффициенты. Логарифмируя данное выражение, получим

Приняв обозначения
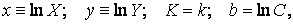
придем к зависимости вида (16). После определения коэффициентов K и b одним из описанных выше способов, найдем параметры исходной зависимости:
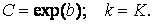
Экспоненциальная зависимость. Многие физические явления и процессы (движение тела в вязкой среде, затухающие колебания, радтоактивный распад, поглощение излучения веществом и др.) описываются дифференциальными уравнениями, решение которых приводит к экспоненциальной (показательной) зависимости между физическими величинами х и Y :
Y = С×exp(K x).