Все Студенту - шпоры, доклады, рефераты, лабораторные, ргр

− 4.3.4. Частотный критерий устойчивости Найквиста

Этот критерий, разработанный в 1932 году американским ученым Г. Найквистом, дает правила, согласно которым по виду частотной характеристики разомкнутой цепи (W_гл(jw)) можно судить об устойчивости замкнутой системы.

Рассмотрим структурную схему САУ в виде:

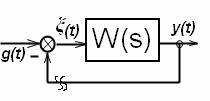
Рис. 4.14

Передаточная функци

− 4.3.5. Анализ устойчивости одноконтурных САУ по их логарифмическим частотным характеристикам

Построение ЛАЧХ разомкнутых систем, особенно асимптотических ЛАЧХ, значительно проще, чем построение годографа АФЧХ. Поэтому в инженерной практике широкое применение получил анализ устойчивости САУ, основанный на построении ЛАЧХ и АФЧХ разомкнутой системы.

Рассмотрим сначала случаи: разомкнутая цепь системы устойчива или нейтральна (астатическая замкнутая система). Как устано

− 4.3.6. Устойчивость систем с запаздыванием

Системы автоматического управления могут содержать звенья, в которых зависимость между входной величиной х(t) и выходной y(t) имеет вид: y(t)=x(t-τ), где τ – постоянная величина, называемая временем запаздывания.

Передаточная функция запаздывающего звена W_зап(S)=.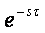

Звен

− 5.1. Прямые оценки качества переходного процесса

К прямым оценкам качества относят:

1. Время переходного процесса (время регулирования) – t_пер.пр., минимальное время, по истечении которого регулируемая величина будет оставаться близкой к установившемуся значению с заданной точностью 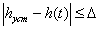. Величина D задается обычно в процентах от установившегося знач

− 5.2. Приближенная оценка вида переходного процесса по вещественной частотной характеристике P(w) замкнутой системы

Установлена связь между вещественной частотной характеристикой P(w) замкнутой САУ и ее переходным процессом h(t).

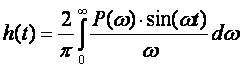(5.5)

Существуют приближенные способы построения кривой переходного процесса в замкнутой системе по этой формуле [ 2 ].

Пусть веществе