2.5.Определение статической характеристики измерительного устройства в нормальных и рабочих условиях.
При эксплуатации измерительного устройства на него действуют различные внешние факторы - влияющие физические величины (см. стр.5), которые не измеряются данным измерительным устойством, однако могут влиять на результаты измерений. Такими величинами чаще других являются окружающая температура, атмосферное давление, вибрация, напряжение питания, влажность воздуха и т.д. Во многом это влияние определяется условиями применения измерительного устройства. В связи с этим принято различать основную и дополнительную погрешности измерительных устройств.
Основная погрешность средства измерений (в том числе измерительных устройств) - это погрешность при его использовании в нормальных условиях.
Нормальными условиями применения средства измерений называют условия, при которых влияющие величины имеют номинальные значения или находятся в пределах нормальной области значений. Нормальные условия применения указываются в стандартах или технических условиях на средства измерений. При использовании средств измерений в нормальных условиях считают, что влияющие на них величины практически никак не изменяют их характеристик.
Дополнительная погрешность средства измерений - это изменение его погрешности, вызванное отклонением одной из влияющих величин от ее нормативного значения или выходом ее за пределы нормальной области значений. Дополнительная погрешность может быть вызвана изменением сразу нескольких влияющих величин. Иными словами, дополнительная погрешность - это часть погрешности, которая добавляется (имеется в виду алгебраическое сложение) к основной в случаях, когда измерительное устройство применяется в рабочих условиях.
Рабочие условия обычно таковы, что изменения значений влияющих величин для них существенно больше, чем для нормальных условий, т.е. область рабочих условий включает в себя область нормальных условий.
Появление дополнительной погрешности является следствием изменения статической характеристики измерительного устройства.
Наглядно отразить изменения погрешностей измерительных устройств под действием влияющих величин можно, используя представление о номинальной и реальной функциях преобразования измерительного устройства (см. стр.13).
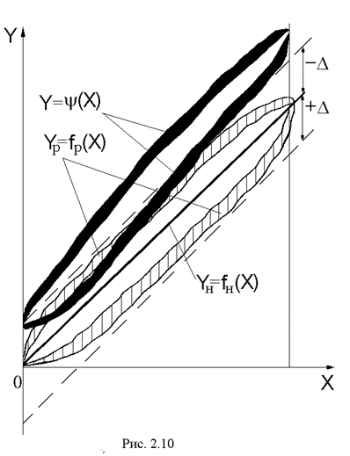
Предположим, что при эксплуатации некоторого измерительного устройства в нормальных условиях его реальная функция преобразования имеет вид петлеобразной кривой Yр = fр(X) (рис.2.10а), где заштрихованная полоса определяет случайную погрешность, вызванную изменением влияющих величин в допустимых нормальными условиями пределах. При этом предполагается, что номинальная функция преобразования Yн = fн(X) этого измерительного устройства (зависимость между входной X и выходной Y величинами в статическом режиме работы) представляет собой прямую (обычно для измерительных устройств устанавливается значение основной погрешности D). На рис.2.10а это показано графически в виде полосы шириной ±D. Если измерительное устройство эксплуатируется в рабочих условиях, когда значение одной или нескольких влияющих величин выходит за пределы, соответствующие значениям при нормальных условиях, функция преобразования выходит за установленное для данного измерительного устройства значение полосы основной погрешности (петлеобразная кривая Y = Y(X) рис.2.10а), т.е. появляется дополнительная погрешность.
Предусмотрено изучение работы измерительных устройств в нормальных и рабочих условиях на примере измерительного преобразователя.
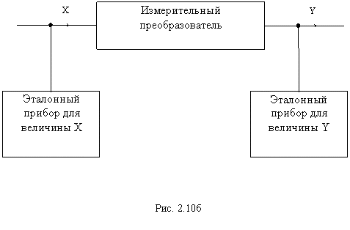
Для измерительных преобразователей по форме представления принято определять абсолютную и приведенную погрешности. В силу того, что результат измерений измерительным преобразователем может представляться в единицах входной и выходной величин, для этих измерительных устройств различают погрешности по входу и выходу. При определении этих погрешностей необходимо знать приписанную данному измерительному преобразователю функцию преобразования (градуировочную характеристику) Yн = fн(X), а для определения погрешности при испытаниях преобразователя необходимо на его входе и выходе осуществить измерение входной X и выходной Y величин с помощью соответствующих эталонных приборов (см. рис. 2.10б).
Абсолютной погрешностью измерительного преобразователя по выходу Dy называют разность между действительным значением величины Yп на выходе преобразователя, отображающей измеряемую величину, и значением Yд величины на выходе, определяемым по действительному значению величины на входе с помощью градуировочной характеристики, приписанной преобразователю:
| Dy = Yп - Yд , | (2.20) |
где Yп - значение выходного сигнала преобразователя при определенном значении входного сигнала;
Yд - значение выходного сигнала, который должен вырабатываться преобразователем, лишенным погрешности, при том же значении входного сигнала.
 |
Значение Yп определяют с помощью эталонного средства измерений, а значение Yд рассчитывают с помощью функции преобразования по действительному значению входной величины Xд, которое воспроизводится мерой или определяется с помощью соответствующего эталонного средства измерений:
| Yд = f(Xд) . | (2.21) |
Из (2.20) и (2.21) находим:
| Dy = Yп - f(Xд) . | (2.22) |
|
Абсолютной погрешностью измерительного преобразователя по входу Dx называют разность между значением Xп величины на входе преобразователя, определяемым по действительному значению Yд величины на его выходе с помощью градуировочной характеристики, приписанной преобразователю, и действительным значением Xд величины на входе преобразователя:
| Dx = Xп - Xд . | (2.23) |
Значение Xд определяется с помощью соответствующего эталонного средства измерений или воспроизводится мерой, а значение Xп определяется по значению Yп выходного сигнала с помощью функции преобразования, решенной относительно X, т.е. Xп = j(Yп) (j - символ обратной функции преобразования). Таким образом,
| Dx = j(Yп) - Xд . | (2.24) |
Приведенной погрешностью измерительного преобразователя по входу (выходу) называют отношение абсолютной погрешности к нормирующему значению входного XN (выходного YN) сигнала:
gx = 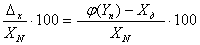 , , |
(2.25) |
gy = 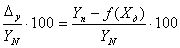 , , |
(2.26) |
где gx и gy - приведенная погрешность измерительного преобразователя по входу и выходу соответственно.
Обычно в качестве нормирующего значения используется диапазон измерений преобразователя Xв - Xн (Xв и Xн - верхний и нижний пределы измерений по входу) или соответствующий ему диапазон измерений выходного сигнала Yв - Yн (Yв и Yн верхний и нижний пределы измерений по выходу). Тогда
gx =  , , |
(2.27) |
gy = 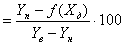 . . |
(2.28) |
Для измерительных преобразователей с линейной функцией преобразования вида Y - Yн=K(X - Xн) приведенные погрешности по входу и выходу в соответствии с (2.27) и (2.28) определяются выражениями:
gx 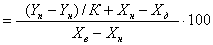 , , |
(2.29) |
gy 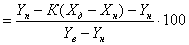 , , |
(2.30) |
где К - коэффициент преобразования измерительного преобразователя, определяемый отношением (Yв - Yн)/(Xв - Xн).
Общая погрешность gобщ может быть определена по формуле:
| gобщ = g + gдоп . | (2.31) |
Формула (2.31) записана для приведенных основной g и дополнительной gдоп (по входу или выходу) погрешностей, значения которых подставляются в эту формулу со своими знаками.
Ввиду того, что в общем случае функция преобразования измерительного преобразователя может иметь петлеобразную форму (рис.2.10а), что связано с явлением гистерезиса (см. стр.13), принято определять вариацию измерительного преобразователя. Обычно определяют приведенную вариацию.
Приведенная вариация измерительного преобразователя по входу (выходу) - отношение (в процентах) максимальной (в диапазоне измерений) разности сигналов по входу (выходу), имеющей место при одном и том же из ряда принятых при испытаниях значений измеряемой величины при постепенном увеличении (прямой ход) и уменьшении (обратный ход) этой величины, к диапазону измерений по входу (выходу).
Вариация по входу:
Wпx = 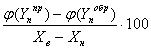 , , |
(2.32) |
вариация по выходу:
Wпу = 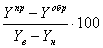 , , |
(2.33) |
где Yпр,Yобр - выходной сигнал измерительного преобразователя при прямом и обратном ходе.
Класс точности L (см. понятие класса точности на стр. 27) измерительного преобразователя нормируется обычно приведенной погрешностью.
Так как измерительные преобразователи обычно имеют линейную функцию преобразования, то класс точности их определяется выражениями (2.29) и (2.30).