3.1.Общие сведения об измерениях
Эксперимент (от лат. experimentum - "проба", "опыт") - метод познания, с помощью которого исследуются реальные явления действительности, реальные функциональные связи между параметрами, характеризующими состояние изучаемого объекта.
В технике и точных науках эксперимент связан с измерениями. Поэтому его называют измерительным экспериментом.
Измерительный эксперимент включает в себя подготовку, проведение измерений и обработку полученных экспериментальных данных.
Проведение измерительного эксперимента должно быть основано на применении известной (типовой) или специально разработанной (частной) методике выполнения измерений.
Методика выполнения измерений (методика измерений) - это совокупность метода, средств, процедур и условий подготовки и проведения измерений, а также правил обработки результатов измерений. Методики выполнения измерений разрабатываются метрологическими службами.
В метрологии все измерения подразделяются в зависимости от вида уравнения измерения, что и определяет способ получения результата. Различают прямые, косвенные, совокупные и совместные измерения.
Прямыми называют измерения, при которых искомое значение величины находят непосредственно из опытных данных. Математически прямое измерение описывается следующим уравнением:
| X = A[X] , | (3.1) |
где X - измеряемая физическая величина;
А - числовое значение физической величины;
[X] - единица физической величины.
Косвенными называют измерения, при которых искомое значение величины находят на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям. При косвенных измерениях путем прямых измерений находят значения величин-аргументов, а значение измеряемой величины Y определяют путем вычислений по формуле:
| Y = f(X1, X2, ... , Xj, ..., Xm) , | (3.2) |
где X1, X2, ... , Xj, ..., Xm - величины-аргументы.
Совокупными называют проводимые одновременно измерения нескольких одноименных величин, при которых искомое значение величины находят решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин или ряда других величин, функционально связанных с искомыми.
Совместными называют проводимые одновременно измерения двух или нескольких неодноименных величин для нахождения зависимости между ними. Получение результатов совместных измерений также связано с необходимостью составления и решения системы уравнений.
Все перечисленные виды измерений (прямые, косвенные, совокупные и совместные) по числу измерений, проводимых для получения результата, могут быть однократными (обыкновенными) и многократными (статистическими).
При постановке измерительного эксперимента прежде всего требуется определить, какие (однократные или многократные) измерения следует осуществлять для определения значения измеряемой физической величины.
Общим здесь является следующий подход:
- если систематическая погрешность (понятия систематической и случайной погрешностей см. на стр.5-6) является определяющей, т.е. ее значение существенно больше значения случайной погрешности, то целесообразно использовать однократные измерения для получения значения измеряемой величины;
- если случайная погрешность является определяющей, то необходимо использовать многократные измерения.
Чрезвычайно важным при выборе многократных и однократных измерений является представление о диффузионности физической величины, под которой понимают невоспроизводимость значений величины от опыта к опыту.
Разброс результатов измерений в общем случае описывается выражением:
Dр =  , , |
(3.3) |
где 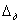 - диффузионность физической величины;
- диффузионность физической величины;
 - абсолютная погрешность средства измерений.
- абсолютная погрешность средства измерений.
Абсолютную погрешность средства измерений  можно принять равной половине цены деления шкалы аналогового прибора или единице младшего разряда цифрового прибора.
можно принять равной половине цены деления шкалы аналогового прибора или единице младшего разряда цифрового прибора.
Из выражения (3.3) можно количественно определить соотношение между  и
и 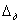 , при котором следует проводить однократные и многократные измерения, а именно:
, при котором следует проводить однократные и многократные измерения, а именно:
- если 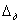 >>
>>  , то необходимо использовать многократные измерения (как правило, целесообразно исходить из соотношения
, то необходимо использовать многократные измерения (как правило, целесообразно исходить из соотношения 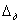 >3
>3  );
);
- если 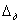 <<
<<  , то необходимо использовать однократные измерения (как правило, целесообразно исходить из соотношения
, то необходимо использовать однократные измерения (как правило, целесообразно исходить из соотношения 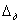 < 1/3
< 1/3  );
);
- если 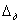 »
»  , то целесообразно использовать однократные измерения, а полученную погрешность увеличить в 1.5 раза (такой вывод следует из выражения (3.3) при замене в нем
, то целесообразно использовать однократные измерения, а полученную погрешность увеличить в 1.5 раза (такой вывод следует из выражения (3.3) при замене в нем 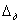 на
на  , при которой Dр » 1.4
, при которой Dр » 1.4 ).
).
Определение соотношения 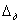 < 1/3
< 1/3  по шкале измерительного прибора затруднительно, поэтому, если
по шкале измерительного прибора затруднительно, поэтому, если 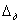 не превышает 0.2 деления шкалы аналогового прибора, или изменения цифры младшего разряда цифрового прибора не превышает единицы, считается, что в данном случае целесообразно проводить однократные измерения.
не превышает 0.2 деления шкалы аналогового прибора, или изменения цифры младшего разряда цифрового прибора не превышает единицы, считается, что в данном случае целесообразно проводить однократные измерения.
При выполнении измерений необходимо учитывать тот факт, что систематическая погрешность вызывает смещение результатов измерений и является наиболее опасной, так как во многих случаях о ее существовании даже не подозревают.
Обнаружение систематической погрешности измерений является одной из наиболее сложных задач метрологии. В том или ином виде ее приходится решать при подготовке измерений.
Близость к нулю систематической погрешности определяется как правильность измерений. Исключение систематической погрешности из результатов измерений рассматривается как исправление этих результатов. Поэтому результаты измерений, содержащие неисключенную систематическую погрешность, называют неисправленными, а результаты, в которых систематическая погрешность исключена, - исправленными.
В настоящее время для обработки экспериментальных данных многократных измерений принято использовать методы математической статистики. При этом следует помнить, что применение этих методов позволяет получить корректные результаты только в том случае, когда из экспериментальных данных исключены систематические погрешности или учтены рекомендации, вытекающие из выражения (3.3).