Все Студенту - шпоры, доклады, рефераты, лабораторные, ргр

.

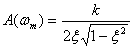Максимуму АЧХ соответствует частота

,

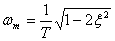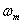( определяется из выражения ).

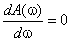ЛАЧХ строится по уравнениям двух асимптот:

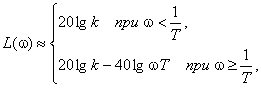
где 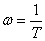- сопрягающая частота.

Асимптотическая ЛАЧХ (рис. 3.9) при 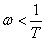параллельна оси частот, а при имеет наклон - 40 дБ/дек.

При коэффициентах демпфирования точная ЛАЧХ отличается от асимптотической. На частоте необходимо вычислять превышение (поправку) . Имеются шаблоны для вычерчивания этой кривой. В упрощенных расчетах достаточно находить при .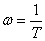

При расхождение между асимптотическими и истинными ЛАЧХ не превышает 3 дБ. Снижение параметра затухания приводит к повышению колебательности переходного процесса и росту резонансного пика амплитудной частотной характеристики.

Как показано выше, по частотным характеристикам можно определить параметры колебательного звена.

Апериодическое звено второго порядка ()

Передаточную функцию колебательного звена в этом случае можно преобразовать к виду

,

т.е. это звено является последовательным соединением двух апериодических звеньев первого порядка и не относится к числу элементарных звеньев.

Консервативное звено()

Передаточная функция .

АФЧХ: .

АЧХ: , ФЧХ:

ЛАЧХ:

Частотные функции представлены на рис. 3.10.

Рис. 3.10. Частотные и переходная характеристики консервативного звена

Переходная функция представляет собой график гармонических колебаний (рис. 3.10).

.