Все Студенту - шпоры, доклады, рефераты, лабораторные, ргр

В ТАУ приняты следующие формы записи линеаризованных дифференциальных уравнений звеньев.

1. Операторный (символический) способ записи.

- Операцию дифференцирования по времени обозначают .

- Выходную величину и ее производные оставляют слева.

- Коэффициент при приращении выходной величины делают равным единице (делением всех членов уравнения на ).

- Вводят постоянные времени , .

- Вводят коэффициенты передачи , .

- Опускают в уравнении символ .

Уравнение (3.7) в этом случае будет иметь вид

(3.8)

В установившемся состоянии, когда и из уравнения (3.8) получаем уравнение статики данного звена

и соответствующую линейную статическую характеристику звена.

Коэффициент показывает отношение выходной величины к входной в установившемся режиме, его размерность определяется отношением размерности к размерности .

2. Форма записи с помощью передаточной функции.

Введем обозначения:

,

.

Многочлен называют собственным оператором звена, многочлен - входным оператором.

Название “собственный оператор” обусловлено тем, что многочлен характеризует собственное движение звена, т.е. его движение при отсутствии внешних возмущающих и управляющих воздействий.

Уравнение звена теперь можно представить в форме

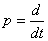, . (3.9)

Вводится формальное определение передаточной функции звена, описываемого линейным дифференциальным уравнением с постоянными коэффициентами:

. (3.10)

Символическая запись уравнения (3.8) будет иметь вид:

, здесь .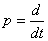

Не следует путать символ дифференцирования с комплексной переменной (или ), имеющей место в преобразовании Лапласа ().

В отличие от преобразования Лапласа, операторный способ, сокращая запись дифференциальных уравнений, не дает способа для их решения.

Более строго определение передаточной функции вводится на базе преобразования Лапласа:

, .

Пусть даны начальные условия

, , .

Тогда

, ,

.

Применив это преобразование к дифференциальному уравнению звена (3.8), получим

.

Из этого алгебраического выражения найдем изображение выходной величины

,

где через обозначен многочлен, включающий в себя все члены с величинами начальных условий.

Передаточной функцией звена называется отношение изображений Лапласа выходной и входной величин при нулевых начальных условиях и равных нулю остальных воздействий на звено, т.е.

, (3.11)

Сравнивая полученное выражение (3.11) с дифференциальным уравнением звена (3.8), видим, что формально передаточную функцию звена можно составлять как отношение операторных многочленов правой и левой частей уравнения звена, сделав замену оператора на оператор .

Это следует из того, что дифференцированию оригинала – символическому умножению оригинала на , при нулевых начальных условиях соответствует умножение изображения переменной на комплексное число .

Сходство между передаточными функциями в операторной форме и в форме изображения Лапласа чисто внешнее, и оно имеет место только в случае стационарных звеньев (и систем).

В общем случае, степень многочлена , как правило, ниже степени многочлена 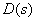. Характеристическое уравнение звена имеет вид , так что корни характеристического уравнения звена являются полюсами его передаточной функции.

Понятием передаточной функции удобно пользоваться при анализе структурных схем САУ.