3.2. Динамические звенья и их характеристики
Для расчета различных систем автоматического управления они обычно разбиваются на динамические звенья.
Под динамическим звеном понимают устройство любого физического вида и конструкции, но описываемое определенным дифференциальным уравнением.
(Другое определение: Динамическое звено – это часть САУ, соответствующая какому-либо элементарному алгоритму).
В соответствии с этим определением классификация звеньев производится по виду дифференциального уравнения (или передаточной функции).
У каждого динамического звена может быть лишь одна входная и выходная величина. Выходная величина всякого динамического звена не оказывает на него какого-либо влияния, т.е. динамические звенья имеют свойство однонаправленности.
Статическая характеристика любого линеаризованного звена может быть изображена прямой линией.
В соответствии со статической характеристикой различают типы динамических звеньев.
В звеньях позиционного, или статического, типа линейной зависимостью 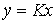 связаны выходная и входная величины в установившемся режиме. Коэффициент
связаны выходная и входная величины в установившемся режиме. Коэффициент 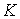 называют коэффициентом передачи звена.
называют коэффициентом передачи звена.
В звеньях интегрирующего типа линейной зависимостью 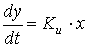 связаны производная выходной величины и входная величина в установившемся режиме. В этом случае для установившегося режима будет справедливо равенство
связаны производная выходной величины и входная величина в установившемся режиме. В этом случае для установившегося режима будет справедливо равенство 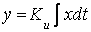 , откуда и произошло название этого типа звеньев.
, откуда и произошло название этого типа звеньев.
При одинаковой размерности входной и выходной величин коэффициент передачи 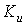 будет иметь размерность [сек -1].
будет иметь размерность [сек -1].
В звеньях дифференцирующего типа линейной зависимостью 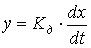 связаны выходная величина и производная входной величины в установившемся режиме, откуда и произошло название этого типа звеньев. При одинаковой размерности входной и выходной величин коэффициент передачи
связаны выходная величина и производная входной величины в установившемся режиме, откуда и произошло название этого типа звеньев. При одинаковой размерности входной и выходной величин коэффициент передачи 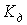 будет иметь размерность [сек].
будет иметь размерность [сек].
В дальнейшем изложении для характеристики звеньев используем в основном передаточные функции типовых динамических звеньев, которые имеют в числителе и знаменателе полиномы от S не выше второго порядка.
Передаточную функцию типового динамического звена в общем случае можно представить как произведение сомножителей следующего вида:
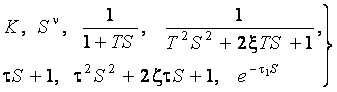 (3.12)
(3.12)
где 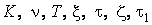 – постоянные, причем
– постоянные, причем 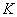 >0, показатель степени
>0, показатель степени 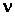 может быть положительным и отрицательным целым числом,
может быть положительным и отрицательным целым числом, 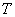 > 0,
> 0, 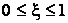 ,
, 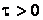 ,
, 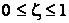 ,
, 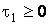 .
.
В соответствии с видом сомножителей (3.12) в таблице 3.1 приведены типовые динамические звенья.
Таблица 3.1
Типовые динамические звенья
(k — передаточный коэффициент; T, τ — постоянные времени; 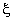 — коэффициент демпфирования: р = d/dt оператор дифференцирования; S – комплексная величина преобразования Лапласа)
— коэффициент демпфирования: р = d/dt оператор дифференцирования; S – комплексная величина преобразования Лапласа)
| Тип звена | Дифференциальное уравнение | Передаточная функция
W=W(S) |
|
| Идеальное усилительное (безынерционное) | y=ku | W=k | |
| Позиционные звенья | Апериодическое (инерционное) | (Tp+1)y= ku | 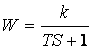 |
| Апериодическое (инерционное)
второго порядка |
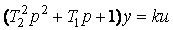 |
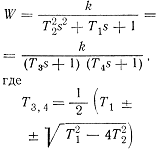 |
|
| Колебательное | 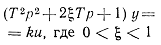 |
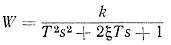 |
|
| Консервативное | 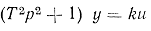 |
 |
|
| Интегрирующие | Интегрирующее
идеальное |
py=ku | 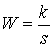 |
| Интегрирующее
инерционное |
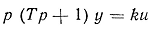 |
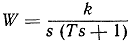 |
|
| Изодромное | 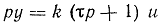 |
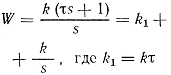 |
|
| Изодромное
второго порядка |
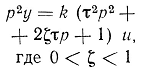 |
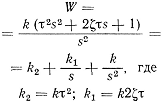 |
|
| Дифференцирующие звенья | Дифференцирующее
идеальное |
y=kpu | W=ks |
| Дифференцирующее
инерционное Форсирующее идеальное |
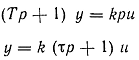 |
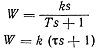 |
|
| Форсирующее
идеальное второго порядка |
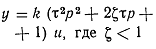 |
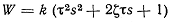 |
|
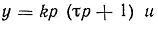 |
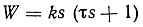 |
||
3.2.1. Временные характеристики. Переходная функция. Функция веса
3.2.2. Частотная передаточная функция и частотные характеристики динамического звена
3.2.3. Логарифмические частотные характеристики
3.2.4. Характеристики позиционных звеньев