4.3.6. Устойчивость систем с запаздыванием

ТАУ » 4. Устойчивость систем автоматического управления. Критерии устойчивости » 4.3. Частотные критерии устойчивости. Принцип аргумента » 4.3.6. Устойчивость систем с запаздыванием

Метки: Рисунок, САУ, система, время, процесс, параметры, устойчивость, критерий, величина

Системы автоматического управления могут содержать звенья, в которых зависимость между входной величиной х(t) и выходной y(t) имеет вид: y(t)=x(t-τ), где τ – постоянная величина, называемая временем запаздывания.

Передаточная функция запаздывающего звена W_зап(S)=.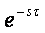

Звенья с чистым запаздыванием часто встречаются в различных технологических процессах, когда материал перемещается из одной точки в другую с помощью ленточных транспортеров; в системах регулирования толщины листа при прокатке; в системах магнитной записи и воспроизведения и т. д.

Процессы в САУ с запаздыванием описываются дифференциально-разностными уравнениями.

4.25.

Во многих тепловых процессах, а также в процессах, в которых происходит передача сигналов на расстояние при помощи длинных электрических, гидравлических и других линий наблюдают запаздывание, распределенное по всей длине линии, которое в отличие от чистого запаздывания приводит к искажению передаваемых сигналов. Системы, содержащие звенья с распределенным запаздыванием, требуют для своего описания дифференциальных уравнений в частных производных.

На практике широко применяют апроксимацию передаточных функций сложных систем с распределенными параметрами при помощи передаточных функций систем с сосредоточенными параметрами и эквивалентными постоянными времени чистого запаздывания.

Иногда сложные системы высокого порядка с сосредоточенными параметрами, содержащие большое количество инерционных звеньев, также можно заменить для приближенного исследования более простой системой низкого порядка, но содержащей звенья с чистым запаздыванием.

Структурная схема одноконтурной САУ со звеном чистого запаздывания может быть представлена в виде, как показано на рис. 4.26.

а)
б)
	Рис. 4.26. Структурные схемы замкнутых САУ с запаздыванием

Передаточная функция разомкнутой системы с запаздыванием равна:

(4.40)

Если запаздывающее звено находится в прямой цепи, то передаточная функция замкнутой системы:

(4.41)

Если же запаздывающее звено находится в цепи обратной связи , то передаточная функция замкнутой системы:

(4.42)

Из выражений (4.41) и (4.42) видно, что характеристическое уравнение системы в обоих случаях имеет вид: .

Это уравнение из-за наличия множителя является не полиномом, а трансцендентной функцией оператора S и в отличие от обыкновенного алгебраического уравнения имеет бесконечное множество корней. Поскольку , то уравнение (4.43) можно рассматривать как уравнение «бесконечной степени». Нахождение корней этого уравнения затруднительно. Применение критериев Рауса и Гурвица для систем с запаздыванием также непригодно.

Как показал Я. З. Цыпкин, для исследования устойчивости систем с запаздыванием удобно применять критерий устойчивости Найквиста.

Формулировка критерия устойчивости Найквиста для систем с чистым запаздыванием аналогична формулировке для систем без запаздывания, имеющих дробно-рациональные передаточные функции. АФЧХ разомкнутой системы в этом случае:

(4.43)

Из выражения (4.43) видно, что звено запаздывания не меняет модуль А(ω) АФЧХ разомкнутой системы, а вносит лишь дополнительный отрицательный фазовый сдвиг ωτ, пропорциональный частоте ω с коэффициентом пропорциональности, равным времени запаздывания t.

При построении АФЧХ разомкнутой САУ с запаздыванием каждый модуль A(ω_i) вектора АФЧХ - W(jω) поворачивают на угол по часовой стрелке. С ростом частоты ω угол ωτ будет быстро расти, а модуль А(ω) обычно уменьшается, поэтому АФЧХ разомкнутой системы с запаздыванием имеет вид спирали, закручивающейся вокруг начала координат. Условие устойчивости ухудшается, т. к. вся АФЧХ приближается к критической точке (-1,j0).