Все Студенту - шпоры, доклады, рефераты, лабораторные, ргр

Выше уже отмечалось, что обратные связи могут быть положительными и отрицательными. Кроме того, обратные связи могут быть жесткими и гибкими:

a) жесткая обратная связь W_ос(S)=K_ос;

b) инерционная жесткая обратная связь W_ос(S)=;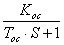

c) гибкая обратная связь W_ос(S)=K_осS;

d) инерционная гибкая обратная связь W_ос(S)= .

Возможны и более сложные передаточные функции корректирующих обратных связей. Гибкая обратная связь действует только в переходном режиме. В установившемся режиме Ф(0)=W₀(0), W_ос(0)=0. Если W_ос(0)≠0, то обратная связь действует не только в переходном, но и в установившемся режиме. В этом случае обратная связь называется жесткой.

Основные свойства этих обратных связей проиллюстрируем на примерах.

Положительная жесткая обратная связь. Пусть она охватывает апериодическое звено (рис. 7.10).

Рис. 7.10

, или , (7.10)

где , .

Из (7.10) видно, что при положительный обратной связи может увеличиваться коэффициент усиления звена, но одновременно с этим увеличивается и постоянная времени. При звено становится неустойчивым.

Отрицательная жесткая обратная связь. При охвате ею инерционного звена имеем , . Постоянная времени звена Т₁ уменьшается, но одновременно с этим уменьшается коэффициент передачи К₁. Связь оказывает стабилизирующее действие, т. е. превращает неустойчивую замкнутую систему в устойчивую (подобно введению производной). Уменьшение коэффициента К₁ может быть скомпенсировано за счет других звеньев.

При охвате интегрирующего звена отрицательной жесткой обратной связью получаем:

, (7.11)

где , .

Звено превращается в апериодическое с коэффициентом усиления, который целиком определяется только обратной связью. Постоянная времени Т₁ будет мала при большом коэффициенте усиления звена К. Звено практически превращается в пропорциональное с коэффициентом К₁. Этот способ введения обратной связи применяется, например, в приводных устройствах, чтобы сделать угол на выходном валу пропорциональным управляющему сигналу (напряжению).

Инерционная жесткая обратная связь. При охвате ею интегрирующего звена имеем:

, , (7.12)

где , , .

Следовательно, в данном случае интегрирующее звено превращается в звено второго порядка с введением производной. Коэффициент усиления К₁ и интенсивность введения производной T_oc целиком определяется обратной связью. При большом К постоянные T₁ и T₂ малы, и мы имеем эквивалентное усилительное звено с введением производной W_экв(S)=K₁(T_ocs+1). Отсюда её хорошее влияние на качество переходного процесса в системе в целом.

Гибкая обратная связь.

а) Пусть заданы объект и обратная связь передаточными функциями , W_OC(S)=K_OCS.

Тогда замкнутый контур будет иметь передаточную функцию , где , .

Как видно, в этом случае увеличивается демпфирование звена (), коэффициент усиления не меняется. При процесс превращается в апериодический.

Заметим, что охватывать гибкой обратной связью апериодическое звено нет смысла, так как это только увеличивает его постоянную времени (инерционность).

б) Пусть задано инерционное интегрирующее звено (интегрирующее звено с замедлением) и гибкая обратная связь:

, W_OC(S)=K_OCS.

Тогда ,

где , ,

т.е. сохраняется тот же тип интегрирующего звена, но с уменьшенной инерционностью (T₁ < T).

Инерционная обратная связь.

Заданы интегрирующее звено с замедлением и инерционная гибкая обратная связь:

, .

Имеем ,

где , , .

При сохранении интегрирующего свойства звена получаем эффект введения производной, т.е. интегрирующее звено становится изодромным, а новые постоянные времени Т₁ и Т₂ могут быть сделаны малыми за счёт большого коэффициента К. В последнем случае имеем:

.

Следует заметить, что инерционное запаздывание в обратной связи (в отличие от такового в прямой цепи) целесообразно использовать для улучшения качества переходных процессов, получая эффект аналогичный введению производной в прямой цепи.