3.2.5. Характеристики интегрирующих звеньев
1. Идеальное интегрирующее звено
Уравнение и передаточная функция:
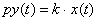или 
,
.
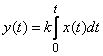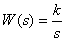Частотные характеристики (рис. 3.11)
АФЧХ: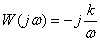 
, 
, 
.
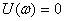АЧХ: 
; ФЧХ: 
.
ЛАЧХ: 
.
Переходная и весовая функции имеют вид (рис. 3.11)
, 
, 
Рис. 3.11. Частотные и временные характеристики интегрирующего звена
Примеры интегрирующих звеньев: операционный усилитель в режиме интегрирования; гидравлический демпфер (вход – сила 
действующая на поршень, выход – перемещение поршня) и т.п.
2. Интегрирующее звено с замедлением (инерциальное нтегрирующее звено)
Уравнение и передаточная функция звена:
, 
.
Частотные характеристики
АФЧХ: 
, 
, 
.
АЧХ: 
; ФЧХ: 
.
ЛАЧХ: 
.
Переходная и весовая функции находятся из решения дифференциального уравнения звена соответственно пр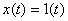и 
и 
. Удобно передаточную функцию представлять в виде алгебраической суммы (в виде двух параллельно включенных звеньев)
,
что позволяет определить решение дифференциального уравнения в виде суммы решений для идеального интегрирующего звена и апериодического звена первого порядка.
,
За счет постоянной времени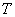 
, вместо идеального интегрирования, здесь получается интегрирование с инерционным запаздыванием. Примером такого звена является электродвигатель, если выходной величиной считать угол поворота вала двигателя.
Асимптотическая ЛАЧХ представляет собой две прямые с отрицательными наклонами – 20 дБ/дек (при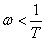 
) и –40 дБ/дек (при 
). ЛАЧХ проходит через точку с координатами 
и 
. Сопряжение асимптот производится на частоте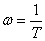 
.
3. Изодромное звено (пропорционально-интегральный закон регулирования). Уравнение и передаточная функция звена:
, 
. (3.41)
Передаточную функцию можно представить в виде произведения
. (3.42)
Из выражения передаточной функции видно, что звено можно условно представить в виде совокупности двух звеньев, действующих параллельно, – безинерционного с коэффициентом передачи 
и идеального интегрирующего с коэффициентом передачи 
.
Частотные характеристики
АФЧХ: 
;
, 
.
АЧХ: 
; ФЧХ: 
.
ЛАЧХ: 
.
Переходная и весовая функции находятся из решения уравнения (3.41)
, (3.42)
, 
.
Асимптотическая ЛАЧХ представляет собой две прямые: с отрицательным наклоном 
(при 
), эта асимптота проходит через точку (,
), и прямой параллельной оси частот (при 
). Из рассмотрения ЛАЧХ и ЛФЧХ видно, что в области частот меньших, чем 
, звено ведет себя как идеальное интегрирующее, а в области частот, больших – как безинерционное с коэффициентом передачи .
Свойство звена вводить интегрирующее действие в области малых частот используется для уменьшения (обнуления) установившейся ошибки в САУ.
Частотные и временные характеристики звена приведены в таблицах 3.2 и 3.3.