4.2. Алгебраические критерии устойчивости. Критерий Гурвица

Вычисление корней характеристического уравнения высокой степени не всегда удобно. Поэтому были выведены критерии устойчивости, позволяющие судить об устойчивости САР непосредственно по коэффициентам характеристического уравнения. В ТАУ наибольшее применение из алгебраических критериев устойчивости получили критерий Рауса и критерий Гурвица.

Задача отыскания критерия устойчивости для систем, описываемых дифференциальными уравнениями любого порядка была сформулирована Максвеллом в 1868 году. Эта задача была впервые решена в алгебраической форме Раусом в 1873 году для уравнений четвертой и пятой степени и полностью – в 1877 году.

Большое распространение получил критерий устойчивости Гурвица, сформулированный им в 1895 году по просьбе словацкого профессора Стодолы, занимавшегося исследованием процесса регулирования турбин.

Предварительно покажем, что необходимым (но не достаточным) условием устойчивости системы является положительность всех коэффициентов характеристического уравнения.

_(4.6)

Если же есть хотя бы один отрицательный коэффициент, то САУ наверняка неустойчива. Действительно, в соответствии с теоремой Безу, уравнение (4.6) можно представить в виде произведения множителей, содержащих корни , , … , характеристического уравнения

. (4.7)

Коэффициент всегда можно сделать положительным.

Пусть все вещественные корни уравнения (4.6) отрицательные, а комплексные корни имеют отрицательные вещественные части (они всегда попарно сопряженные)

, , … , .

Подставив их в уравнение, получим

Средние два сомножителя дают и после перемножения всех скобок получим в уравнении только положительные коэффициенты. Это и требовалось доказать.

Необходимое условие устойчивости становится и достаточным для уравнения первой и второй степени. В этом легко убедится прямым нахождением корней:

1) , ;

2) , .

Для уравнений третьей и выше степеней это условие лишь необходимо, но недостаточно, ибо оно обеспечивает отрицательность только вещественных корней. Комплексные корни могут иметь положительные вещественные части.

Критерий устойчивости Гурвица

Немецким математиком А.Гурвицем был разработан алгебраический критерий устойчивости в форме определителей, составленных из коэффициентов характеристического уравнения системы.

Из коэффициентов характеристического уравнения (4.6) составляют сначала главный определитель Гурвица

(4.8)

по следующему правилу: по главной диагонали определителя от верхнего левого угла выписывают по порядку все коэффициенты, начиная с и заканчивая . Затем каждый столбец определителя дополняют так, что бы вверх от диагонали индексы коэффициентов увеличивались, вниз – уменьшались. В случае отсутствия в уравнении какого-либо коэффициента и вместо коэффициентов с индексом меньше 0 и больше n пишут нуль.

Отчеркивая в главном определителе Гурвица, как показано пунктиром, диагональные миноры, получаем определители Гурвица низшего порядка.

Критерий Гурвица формулируется так:

система автоматического управления устойчива, если при положительны все 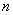определителей Гурвица, получаемых из (4.8), т.е.

; , ; ; … ,

_. (4.9)

Это необходимое и достаточное условие устойчивости.

Предпоследнее неравенство в (4.9) есть , поэтому последнее неравенство сводится к .

Система находится на границе устойчивости, если и все предыдущие определители Гурвица положительны. Условие распадается на два: или . В первом случае система находится на границе апериодической устойчивости (нейтральная устойчивость) (один из корней характеристического уравнения равен нулю); во втором случае – на колебательной границе устойчивости (два сопряженных мнимых корня).

Наконец, граница устойчивости, соответствующая бесконечному корню, будет, согласно уравнению (4.6) при . В самом деле, если все слагаемые в уравнении (4.6) разделить на , то получим

Отсюда видно, что при имеем , а значит .

Раскрывая определители Гурвица для характеристических уравнений первого, второго, третьего и четвертого порядков, можно получить следующие условия устойчивости:

1) для уравнения первого порядка

, условия устойчивости , ; (4.10)

2) для уравнения второго порядка

условия устойчивости

, , , т.е. ; (4.11)

3) для уравнения третьего порядка

, (4.12)

условия устойчивости , , , .

С учетом того, что и коэффициент . Из следует при положительности всех коэффициентов;

4) для уравнения четвертого порядка

, (4.13)

условия устойчивости

, , , ; (4.14)

; ;

Преобразуем

. (4.15)

Таким образом, для уравнений третьего и четвертого порядков, кроме положительности коэффициентов, необходимо соблюдение дополнительных неравенств (4.12) и (4.14).

Для уравнения пятой степени условия устойчивости по критерию Гурвица получаются достаточно громоздкими. Для уравнений высоких порядков () в лучшем случае можно получить ответ о том, устойчива или неустойчива САУ. В случае неустойчивой системы критерий не дает ответа на то, каким образом надо изменять параметры системы, чтобы сделать ее устойчивой. Это обстоятельство привело к поискам других критериев, которые были бы более удобными в инженерной практике.