3.2.4. Характеристики позиционных звеньев
Характеристики позиционных звеньев сведены в таблицы 3.2 и 3.3.
Рассмотрим статические и динамические (временные – h(t) и w(t) и частотные -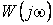 
, 
, 
, 
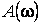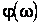) характеристики типовых динамических звеньев.
1. Безынерционное (идеальное усилительное, пропорциональное) звено
В статике и динамике описывается алгебраическим уравнением:
.
Передаточная функция звена:
.
Примерами таких безынерционных звеньев могут служить жесткие механические и гидравлические передачи, электронный усилитель на низких частотах, делитель напряжения, датчики: потенциометрические, индукционные, гироскоп и др.
Переходная функция звена представляет собой ступенчатую функцию, т.е. при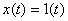 
.
Функция веса 
. АФЧХ вырождается в точку, расположенную на вещественной оси на расстоянии 
от начала координат. Модуль ЧПФ 
постоянен на всех частотах, а фазовые сдвиги равны нулю (
). Безынерционное звено является некоторой идеализацией реальных звеньев. Оно равномерно пропускает все частоты от 0 до 
.
2. Апериодическое (инерционное) звено первого порядка
Дифференциальное уравнение звена:
, 
. (3.24)
Передаточная функция звена:
,
где 
- коэффициент передачи,
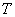- постоянная времени.
Примеры апериодических звеньев:
а) двигатель любого типа (электрический, гидравлический, пневматический), входной величиной является управляющее воздействие (напряжение в ЭД, расход жидкости в ГД и т.п.), выходной величиной является скорость вращения;
б) электрический генератор постоянного тока, входной величиной которого является напряжение, подводимое к обмотке возбуждения, а выходной – напряжение якоря;
в) резервуар с газом, у которого входная величина представляет собой давление 
перед впускным отверстием, а выходная - давление
в резервуаре;
г) нагревательная печь, у которая входная величина – количество поступающего в единицу времени тепла - 
, а выходная – температура в печи - 
;
д) электрические 
и 
цепи.
В установившемся режиме входная и выходная величины связаны уравнением
.
Переходная функция звена является решением дифференциального уравнения при .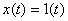
,
, (3.25)
(установившийся режим).
Характеристическое уравнение:
,
откуда корень характеристического уравнения
.
Подставим 
и 
в (3.25):
. (3.26)
Найдем постоянную интегрирования 
, задавшись начальными условиями: при 
, 
. Из (3.26) найдем
.
Окончательно,
. (3.27)
Функция веса звена 
, 
.
На рис. (3.5) представлен график переходной функции звена, показаны параметры и 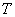, которые можно определить экспериментально из графика. Время переходного процесса в звене определяется обычно, как 
, когда выходное значение в звене устанавливается с ошибкой 
. Постоянная времени характеризует «инерционность», или «инерционное запаздывание» апериодического звена; чем она больше, тем длительнее переходный процесс в звене.
Рис. 3.5. Переходная функция инерционного звена