ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ЗАВИСИМОСТЕЙ часть 3
|
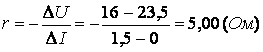 .
.

|
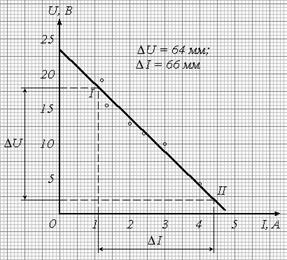
Рис.9. Рис.10
На рис. 9 и 10 графики построены безукоризненно, и величина E = 23,5 В найдена верно. Тем не менее, здесь допущена, по сути дела, одна и та же грубейшая ошибка. Она заключается в том, что при определении тангенса угла наклона прямой не учтен масштаб откладываемых по осям переменных. В обоих случаях получим результаты

не имеющие ничего общего с искомой физической величиной и даже лишенные единиц измерения (только в том случае, когда отрезки DU и DI выражены, соответственно, в вольтах и амперах, их отношение будет иметь размерность Ом). Очевидно, что изменение масштаба графика приведет к изменению реального угла наклона прямой j , что при правильном определении углового коэффициента не должно влиять на

|
получаемый результат.
Рис.11. Рис.12.

|
Ошибки, показанные на рис. 11 и 12, связаны с неудачным выбором масштаба (см. п. 6 правил построения графиков). Сжатие графика по оси ординат (рис.11) приводит к большой погрешности измерения величинE и DU; последнее отрицательно влияет на точность определения r :
E = 21 B;
 ;
;
сжатие по оси абсцисс (рис.12) увеличивает ошибку измерения DI и также приводит к снижению точности нахождения обоих коэффициентов:
E = 24,5 B;
 .
.
Приведенные примеры свидетельствуют о том, что графический способ определения коэффициентов линейной зависимости не свободен от недостатков. Главный из них заключается в том, что проведение сглаживающей прямой носит субъективный характер. Это приводит к тому, что при значительном разбросе экспериментальных данных результат осреднения коэффициентов будет неоднозначным. Как показано на рис. 13, через одни и те же точки можно провести разные прямые – например, 1, 2 и 3, – и тем самым получить различные значения искомых коэффициентов. Причем в ряде случаев полученный результат может противоречить физическому смыслу. Например, если величина х представляет собой момент силы натяжения нити Мн , а у – угловое ускорение крестовины маятника Обербека (работа 1.